Chapter 19 Growth & Animal models

The aim of this document is to explore animal and growth model with generated data to validate their behavior and use it on Symphonia and Eschweilera real data. Let’s consider a set of \(P=3\) populations including each \(Fam=3\) families composed of \(I = 14\) individuals with arbitrar relationships (it’s only 126 individuals to do quick tests).

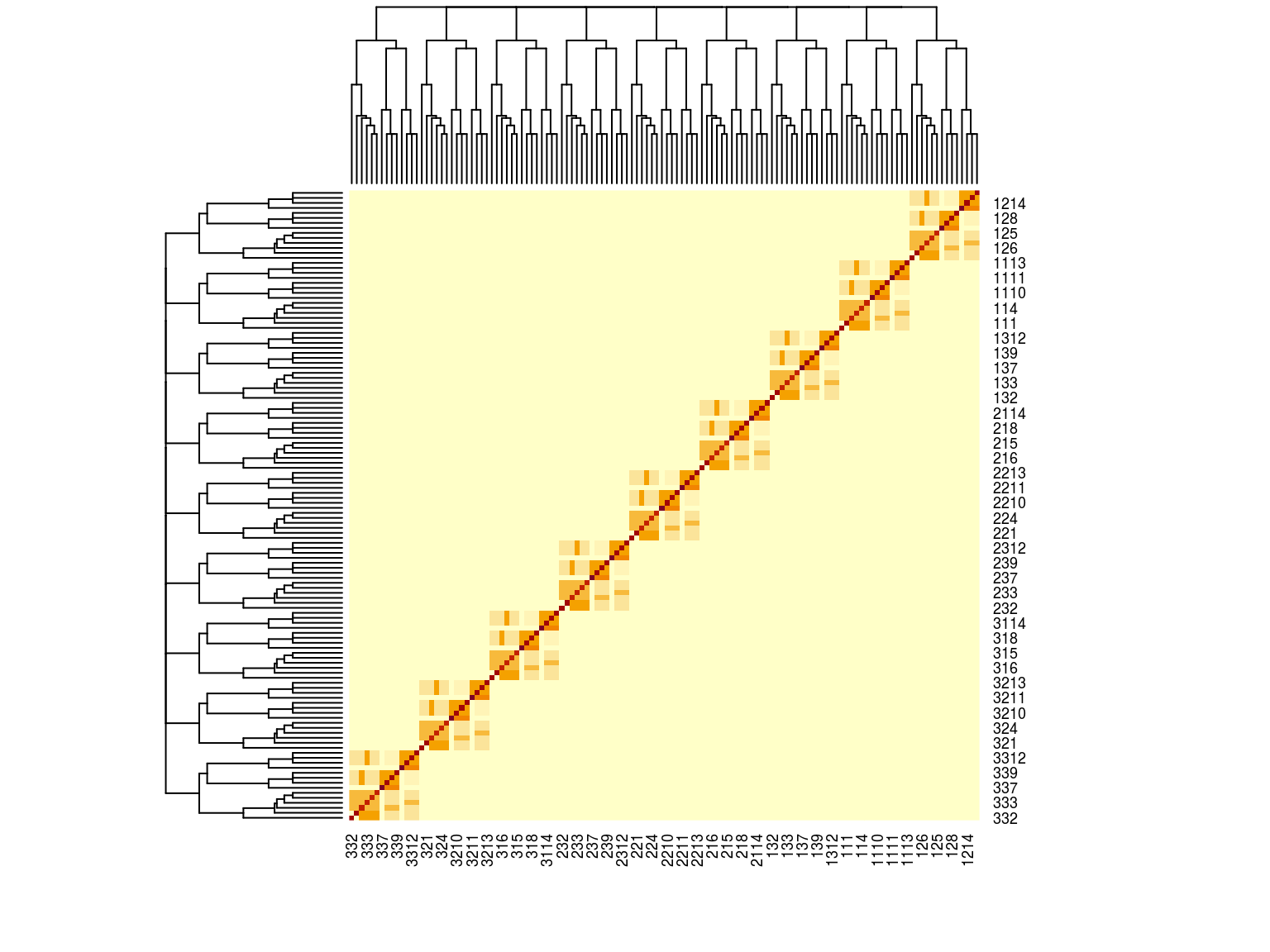
Kinship matrix

Figure 19.1: Kinship matrix

19.1 Animal

We used the following animal model with a lognormal distribution to estimate population and genotypic variance:

\[\begin{equation} y_{p,i} \sim \mathcal{logN}(log(\mu_p.a_{i}),\sigma_1) \\ a_{p,i} \sim \mathcal{MVlogN_N}(log(1),\sigma_2.K) \tag{19.1} \end{equation}\]

We fitted the equivalent model with following priors:

\[\begin{equation} y_{p,i} \sim \mathcal{logN}(log(\mu_p.\hat{a_{i}}), \sigma_1) \\ \hat{a_{i}} = e^{\sqrt{V_G}.A.\epsilon_i} \\ \epsilon_i \sim \mathcal{N}(0,1) \\ ~ \\ \mu_p \sim \mathcal{logN}(log(1),1) \\ \sigma_1 \sim \mathcal N_T(0,1) \\ ~ \\ V_Y = Var(log(y)) \\ V_P = Var(log(\mu_p)) \\ V_R=\sigma_1^2 \\ V_G = V_Y - V_P - V_R \\ \tag{19.2} \end{equation}\]

Table 19.1: Animal model fitted versus expected values.
Parameter Estimate Expected Standard error \(\hat R\)
mu[1] 0.7473821 0.7357714 0.0535640 1.0054690
mu[2] 0.3992248 0.3633681 0.0308554 1.0010121
mu[3] 0.5209272 0.5420625 0.0469693 1.0023625
Vp 0.0702100 0.0841187 0.0151127 1.0011662
Vg 0.0770262 0.0837454 0.0223466 1.0014673
Vr 0.0399184 0.0400000 0.0145103 0.9997977
lp__ 78.5632162 NA 22.6506583 1.0019419
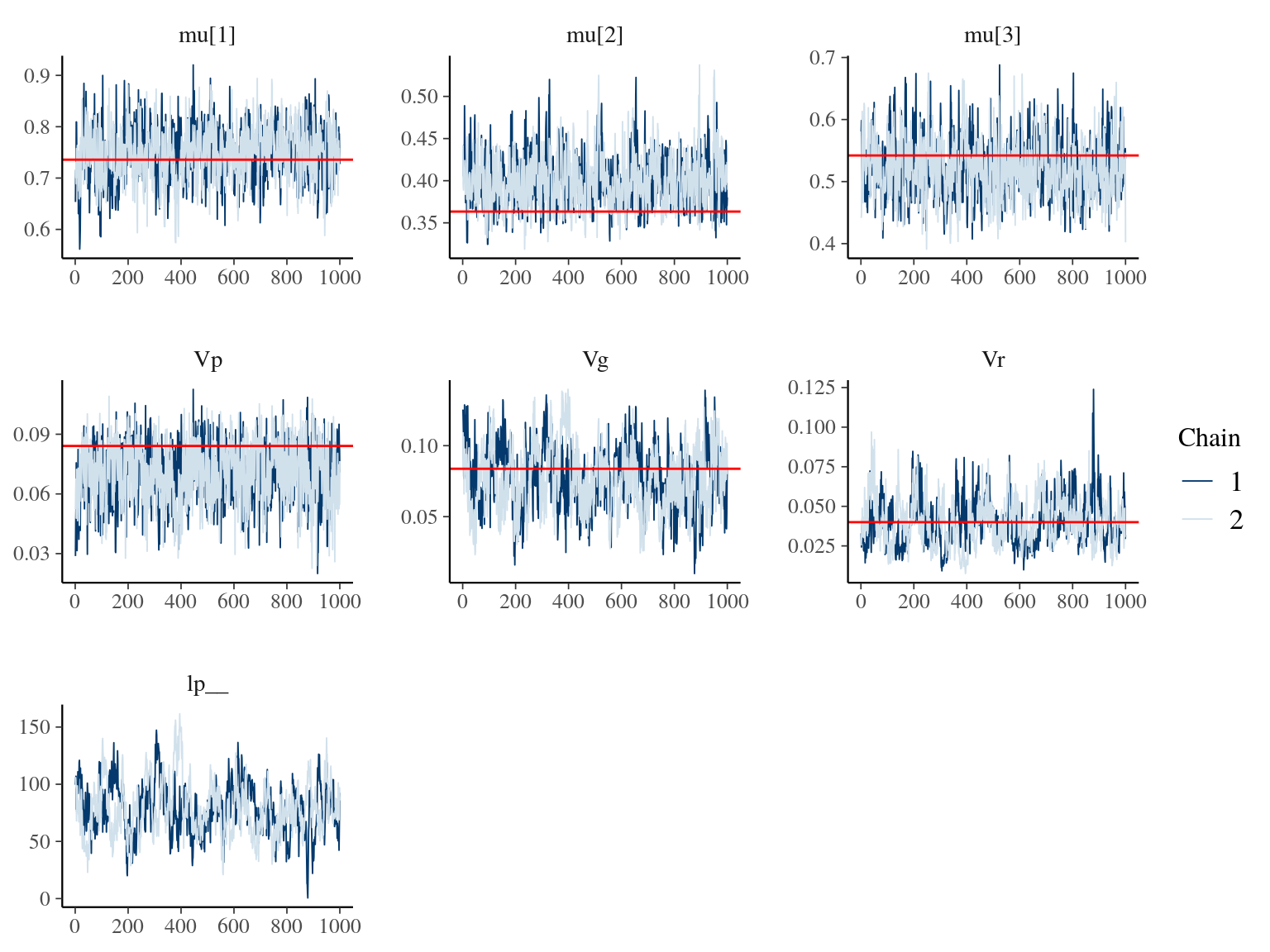
Parameters for Animal model traceplot and expected value in red.

Figure 19.2: Parameters for Animal model traceplot and expected value in red.

19.2 Gmax

We used the following growth model with a lognormal distribution to estimate individual growth potential:

\[\begin{equation} DBH_{y=today,p,i} - DBH_{y=y0,p,i} \sim \\ \mathcal{logN} (log(\sum _{y=y_0} ^{y=today} \theta_{1,p,i}.exp(-\frac12.[\frac{log(\frac{DBH_{y,p,i}}{100.\theta_{2,p}})}{\theta_{3,p}}]^2)), \sigma_1) \\ \theta_{1,p,i} \sim \mathcal {logN}(log(\theta_{1,p}), \sigma_2) \\ \theta_{2,p} \sim \mathcal {logN}(log(\theta_2),\sigma_3) \\ \theta_{3,p} \sim \mathcal {logN}(log(\theta_3),\sigma_4) \tag{19.3} \end{equation}\]

We fitted the equivalent model with following priors:

\[\begin{equation} DBH_{y=today,p,i} - DBH_{y=y0,p,i} \sim \\ \mathcal{logN} (log(\sum _{y=y_0} ^{y=today} \hat{\theta_{1,p,i}}.exp(-\frac12.[\frac{log(\frac{DBH_{y,p,i}}{100.\hat{\theta_{2,p}}})}{\hat{\theta_{3,p}}}]^2)), \sigma_1) \\ \hat{\theta_{1,p,i}} = e^{log(\theta_{1,p}) + \sigma_2.\epsilon_{1,i}} \\ \hat{\theta_{2,p}} = e^{log(\theta_2) + \sigma_3.\epsilon_{2,p}} \\ \hat{\theta_{3,p}} = e^{log(\theta_3) + \sigma_4.\epsilon_{3,p}} \\ \epsilon_{1,i} \sim \mathcal{N}(0,1) \\ \epsilon_{2,p} \sim \mathcal{N}(0,1) \\ \epsilon_{3,p} \sim \mathcal{N}(0,1) \\ ~ \\ (\theta_{1,p}, \theta_2, \theta_3) \sim \mathcal{logN}^3(log(1),1) \\ (\sigma_1, \sigma_2, \sigma_3, \sigma_4) \sim \mathcal{N}^4_T(0,1) \\ ~ \\ V_P = Var(log(\mu_p)) \\ V_R=\sigma_2^2 \tag{19.4} \end{equation}\]

Table 19.2: Animal model fitted versus expected values.
Parameter Estimate Standard error Expected \(\hat R\)
thetap1[1] 0.5300911 0.0976327 0.5300000 1.0084649
thetap1[2] 0.5872973 0.1001450 0.5400000 1.0145937
thetap1[3] 0.3946491 0.0508020 0.3600000 1.0073573
theta2 0.2572377 0.1007272 0.2500000 1.0000859
theta3 0.5907776 0.1029564 0.7000000 0.9991474
Vp 0.0458205 0.0326534 0.0376656 1.0177764
Vr 0.4342078 0.0897607 0.4489000 1.1038441
lp__ 102.6878571 95.9191313 NA 1.6993161
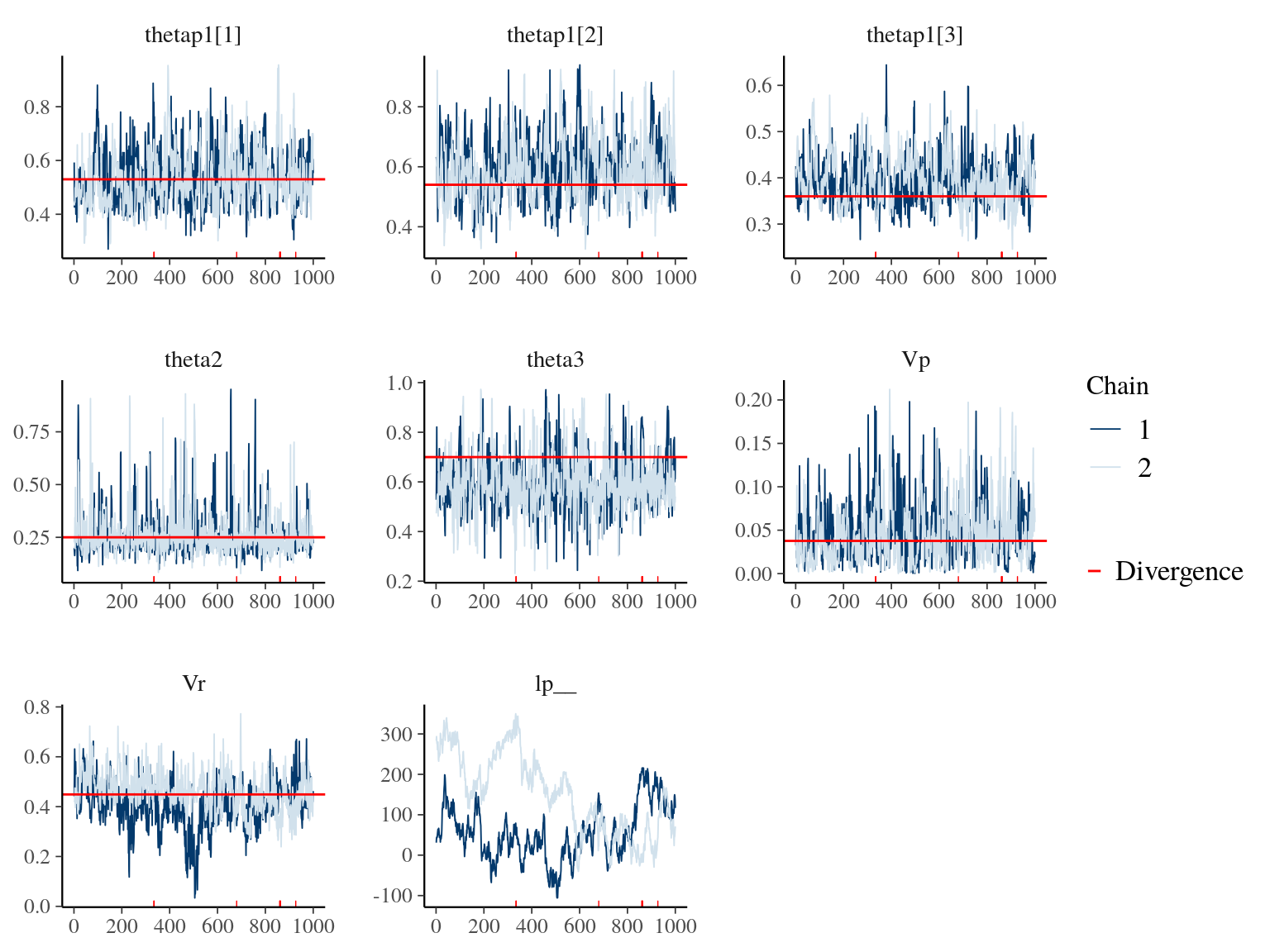
Parameters for Growth model traceplot and expected value in red.

Figure 19.3: Parameters for Growth model traceplot and expected value in red.

19.3 Gmax & Animal

We used the following growth model with a lognormal distribution to estimate individual growth potential and associated genotypic variation:

\[\begin{equation} DBH_{y=today,p,i} - DBH_{y=y0,p,i} \sim \\ \mathcal{logN} (log(\sum _{y=y_0} ^{y=today} \theta_{1,p,i}.exp(-\frac12.[\frac{log(\frac{DBH_{y,p,i}}{100.\theta_{2,p}})}{\theta_{3,p}}]^2)), \sigma_1) \\ \theta_{1,p,i} \sim \mathcal {logN}(log(\theta_{1,p}.a_{1,i}), \sigma_2) \\ \theta_{2,p} \sim \mathcal {logN}(log(\theta_2),\sigma_3) \\ \theta_{3,p} \sim \mathcal {logN}(log(\theta_3),\sigma_4) \\ a_{1,i} \sim \mathcal{MVlogN}(log(1), \sigma_5.K) \tag{19.5} \end{equation}\]

We fitted the equivalent model with following priors:

\[\begin{equation} DBH_{y=today,p,i} - DBH_{y=y0,p,i} \sim \\ \mathcal{logN} (log(\sum _{y=y_0} ^{y=today} \hat{\theta_{1,p,i}}.exp(-\frac12.[\frac{log(\frac{DBH_{y,p,i}}{100.\hat{\theta_{2,p}}})}{\hat{\theta_{3,p}}}]^2)), \sigma_1) \\ \hat{\theta_{1,p,i}} = e^{log(\theta_{1,p}.\hat{a_{1,i}}) + \sigma_2.\epsilon_{1,i}} \\ \hat{\theta_{2,p}} = e^{log(\theta_2) + \sigma_3.\epsilon_{2,p}} \\ \hat{\theta_{3,p}} = e^{log(\theta_3) + \sigma_4.\epsilon_{3,p}} \\ \hat{a_{1,i}} = e^{\sigma_5.A.\epsilon_{4,i}} \\ \epsilon_{1,i} \sim \mathcal{N}(0,1) \\ \epsilon_{2,p} \sim \mathcal{N}(0,1) \\ \epsilon_{3,p} \sim \mathcal{N}(0,1) \\ \epsilon_{4,i} \sim \mathcal{N}(0,1) \\ ~ \\ (\theta_{1,p}, \theta_2, \theta_3) \sim \mathcal{logN}^3(log(1),1) \\ (\sigma_1, \sigma_2, \sigma_3, \sigma_4, \sigma_5) \sim \mathcal{N}^5_T(0,1) \\ ~ \\ V_P = Var(log(\mu_p)) \\ V_G=\sigma_5^2\\ V_R=\sigma_2^2 \tag{19.6} \end{equation}\]

Table 19.3: Animal model fitted versus expected values.
Parameter Estimate Standard error Expected \(\hat R\)
thetap1[1] 0.8158910 0.1121729 0.5300000 1.0008119
thetap1[2] 0.4921939 0.0889950 0.5400000 1.0015447
thetap1[3] 0.3495413 0.0629704 0.3600000 1.0009558
theta2 0.2756253 0.0764302 0.2500000 1.0004898
theta3 0.7269206 0.1440250 0.7000000 0.9996955
Vp 0.1414014 0.0635966 0.0352066 1.0016146
Vg 0.0558953 0.0758363 0.1350074 1.0016744
Vr 0.5172295 0.1090083 0.4489000 1.0170006
lp__ 36.7247279 66.4530270 NA 1.1521719
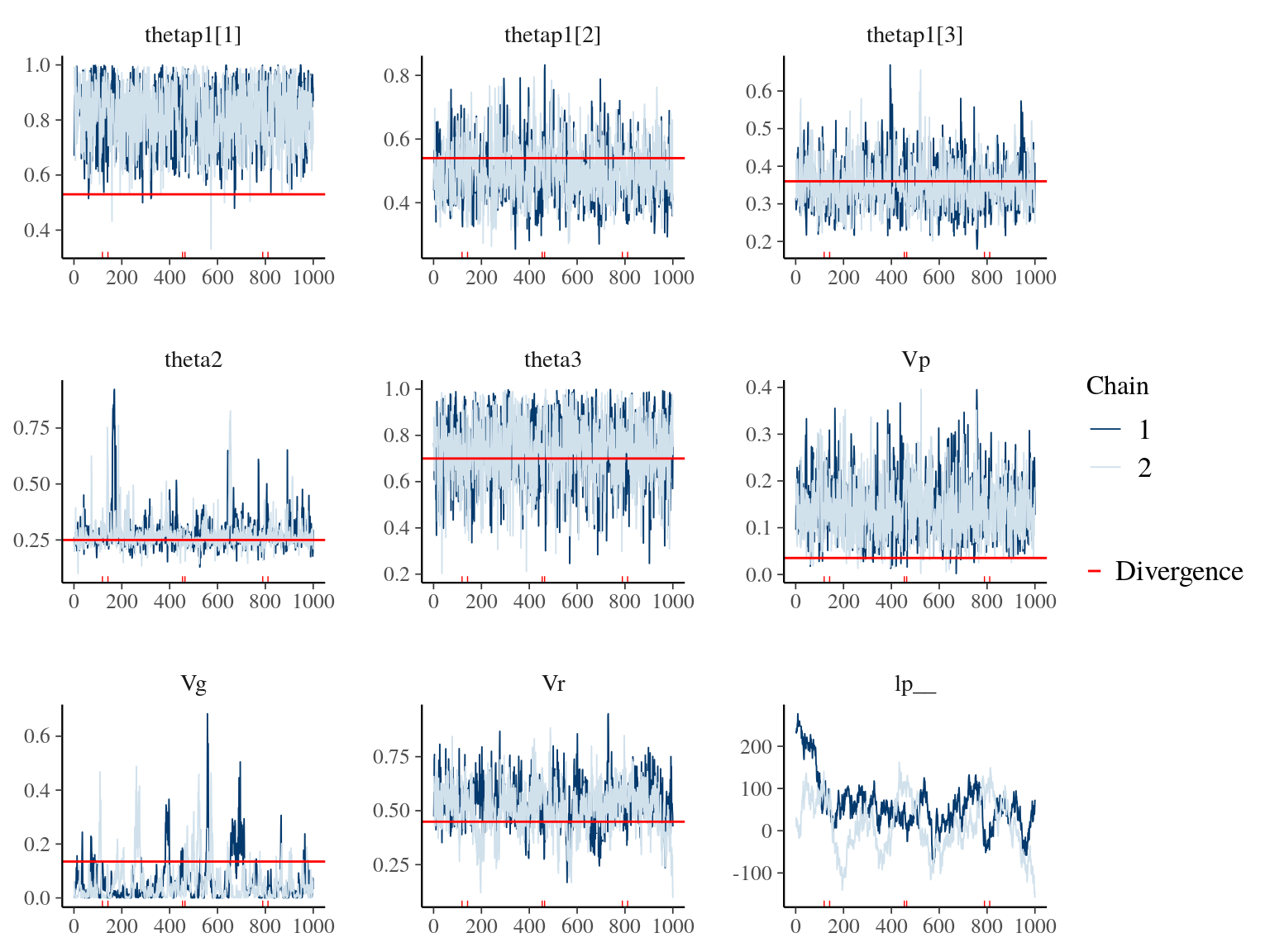
Parameters for Growth & Animal model traceplot and expected value in red.

Figure 19.4: Parameters for Growth & Animal model traceplot and expected value in red.